TextSemanticSimilarity

Idea

The idea of the project is to devsing a metric for measuring semantic similarity between words, sentences and ultimately documents. There are many approaches to this NLP problem- finding out word frequency matrix and applying SVM, reducing the dimensions and finally applying Latent Semantic Analysis to find cosines of row vectors hence measuring the similarity. Our approach is of a corpus-based modeling technique that uses Second Order Co-occurence Pointwise Mutual Information along side certain syntactic similarity measures to measure the overall semantic similarity between two sentences.

Requirements

• Python 3.0+
• NLTK 3.0+

Implementation

Consider two sentences:

s1="The world knows it has lost a heroic champion of justice and freedom"
s2="The earth recognizes the loss of a valliant champoin of independence and justice"

We tokenize, lemmatize and remove stopwords, which gives us a refined list of words:

from Cleaner import clean

#Removing punctuations, stopwords and storing important words in a list
sent1=clean(s1)
sent2=clean(s2)

Cleaner Code

Length of both the lists are maintained:

m=len(sent1)
n=len(sent2)

Common words in both the lists are identified and extracted. These common words are then subtracted from the original lists. Now, the syntactic and semantic similarlity tests measurement methods are operated on the remaing lists given below as s1 and s2. Go on the link below for the Commonwords code:

from Auxiliary import Commonwords, DisplayMatrixform
#Getting the list of common words and the removal of those words from the original list
common,s1,s2=Commonwords(sent1,sent2)

Commonwords Code

Next, we need to find out the syntatic/lexical similarities between list of words in s1 and s2. This is to reduce penalising spelling mistakes. Three measures are taken into consideration:

1. Normalized Longest Common Subsequence(NLCS)- To figure out longest non-consecutive subsequence length. For Example, for semantic and semaantc, it will be 7(semantc). Normalizing is squaring the length of the subsequence and dividing by the product of lengths of the two words.
2. Normalized Longest Common Consecutive Subsequence(NLCCS) from first letter- It takes the longest consecutive subsequence from the firt letter. For the semantic and semaantc it would be 4(sema). It is then normalized.
3. Normalized Longest Common Consecutive Subsequence(NLCCS) from any letter-It takes the longest consecutive subsequence from the firt letter. For the semantic and semaantc it would again be 4(sema). It is then normalized.

Syntactic Similarity Code

These measures are summed over using appropriate weights(which sum to 1) and the final syntactic matrix is created of size length of s1 x length of s2.

synmat={}
if len(s2)<len(s1):
	for i in s2:
		synmat[i]={}
		for j in s1:
			synmat[i][j]=SyntacticSimilarity(i,j)
else:
	for i in s1:
		synmat[i]={}
		for j in s2:
			synmat[i][j]=SyntacticSimilarity(i,j)

Next, we move to calculate the semantic similarity. We use SOC-PMI for the purpose. The details of the method are given in the next section. The SOC- PMI method returns a normalized semantic measure for each combination of words. These measures are stored in a matrix of size length of s1 x length of s2.

if len(s2)<len(s1):
	for i in s2:
		semmat[i]={}
		for j in s1:
			semmat[i][j]=SemanticSimilarity(i,j,a,delta,gamma)
else:
	for i in s1:
		semmat[i]={}
		for j in s2:
			semmat[i][j]=SemanticSimilarity(i,j,a,delta,gamma)

The two matrices are multiplied by weights(sums to 1) and added. The weight decided whether the algorithm stresses on the syntactic or the semantic part or is balanced. The resulting matrix is the searched for maximum value. Once the maximum value is found, it is stored and the row and column containing that column is eliminated. The process is repeated with the remaining matrix till the entire matrix gets eliminated. All the maximum values are summed over.

Similarity Count Code

To calculate the overall sentence similarity, we add the number of common words with the sum of maximum values fetched earlier and multiply it with the sum of length of the two sentences. This is then divided to get by twice the product of lengths of the sentences to derive the final measure.

sentencesimilarity= (len(common)+rhosum)*(m+n)/(2*m*n)
print(sentencesimilarity)

Second Order Co-occurrence Pointwise Mutual Information (SOC-PMI)-

It is a corpus-based learning model. We have used the State Union corpus from the Natural Language ToolKit Corpora. We have trained 20 speeches from the same having approximately 200000 words and about which 13000 are unique (after lemmatizing and excluding all stop words). These are stored as pickles to avoid re-training in future.

#Lemmatizing words and adding to the final array if they are not stopwords
for w in words:
    if w not in stop_words:
	    w=lemmatizer.lemmatize(w)		
	    filtered_text.append(w)

Corpus Training Code

The frequency of each word is stored in a Python dictionary:

typefr=collections.Counter()
	for w in filtered_text:
		typefr[w]+=1

Supppose we need to find semantic similarity between w1 and w2. The frequency of words neighbouring the w1 and w2 are calculated. a neighbours before and after w1 and w2 are taken under consideration.

neighboursw1=collections.Counter()
	n2w1=[]
	for i in range(len(filtered_text)):
		if w1==filtered_text[i]:
			neighboursw1[filtered_text[i]]+=1
			for j in range(0,a+1):
				neighboursw1[filtered_text[i+j]]+=1
				neighboursw1[filtered_text[i-j]]+=1

The PMI values are calculated. And all the neighbour terms are sorted in decreasing order of PMI values. Note that there will be two seperate lists one for w1 and another for w2

pmiw1={}
	for t in neighboursw1.keys():
		pmiw1[t]= math.log(neighboursw1[t]*m/(typefr[t]*typefr[w1]),2)
pmiw1_sorted = sorted(pmiw1, key=pmiw1.get, reverse=True)

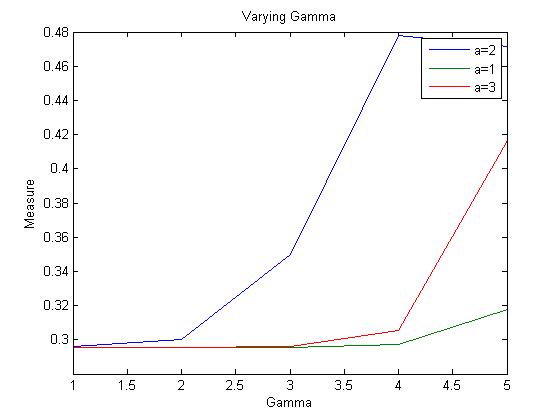
Beta 1 and Beta 2 are calcuated. We have arranged the neighbour words in decreasing order of PMI. Now the values at the back tend to be very small and can be neglected. Hence we select only the first Beta 1 values. These become the feature words. The value of delta has to be selected according to the corpus size. We have chosen a value of 0.7.

b1= math.floor((math.pow(math.log10(typefr[w1]),2)* math.log(len(unique),2))/delta)

Next we sum all the PMIs of the word neighbours common to both w1 and w2. Again two values are maintained one is the Beta summation of w1 and the other of w2. Next, the similarity measure is calculated by dividing betasum1 and betasum2 by beta1 and beta2 respectively and adding both the values. Gamma is selected according to the how much one wants to stress upon the PMI values.

for i in range(0,b1):
		for j in range(0,b2):
			if pmiw1_sorted[i]==pmiw2_sorted[j]:
				betasumw1+=math.pow(pmiw2[pmiw1_sorted[i]],gamma)
similarity= betasumw1/b1 + betasumw2/b2				

The final similarity needs to be normalized between 0 and 1. A lambda value is imported from a local file. The lambda value is updated with the maximum value of PMI the algorithm received in its life time. The normalized similarity measure is then returned.

target=open("Lambda.txt","r")
lmbda=float(target.read())
target.close()

similarity,lmbda= normalized_similarity(similarity,lmbda)

target=open("Lambda.txt","w")
target.write(str(lmbda))
target.close()

return similarity

#Returning Normalized Similarity
def normalized_similarity(similarity,lmbda):
	if similarity>lmbda:
		lmbda=math.ceil(similarity)
	similarity/=lmbda
	return similarity,lmbda

Outputs

Varying Delta

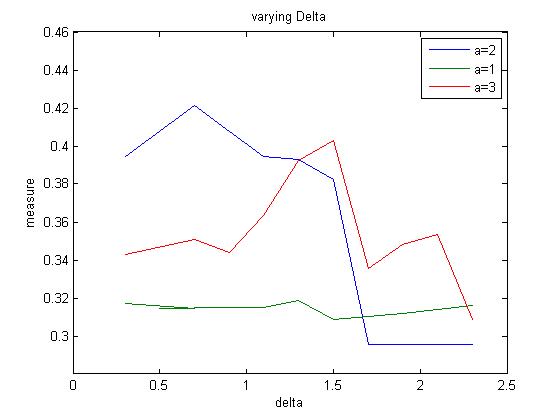
Varying Semantic Similarity Weight measure

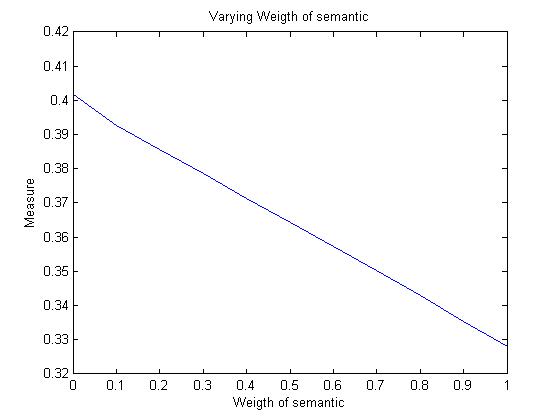
Varying Gamma